

[The Monthly Mean] March/April 2012 -- In defense of surrogate outcomes
The Monthly Mean is a newsletter with articles about Statistics with occasional forays into research ethics and evidence based medicine. I try to keep the articles non-technical, as far as that is possible in Statistics. The newsletter also includes links to interesting articles and websites. There is a very bad joke in every newsletter as well as a bit of personal news about me and my family.
Welcome to the Monthly Mean newsletter for March/April 2012. If you are having trouble reading this newsletter in your email system, please go to www.pmean.com/news/201203.html. If you are not yet subscribed to this newsletter, you can sign on at www.pmean.com/news. If you no longer wish to receive this newsletter, there is a link to unsubscribe at the bottom of this email. Here's a list of topics.
--> In defense of surrogate outcomes
--> Data cleaning on a limited budget
--> Promoting your consulting career in the era of Web 2.0
--> Monthly Mean Article (peer reviewed): Comparison of logistic regression versus propensity score when the number of events is low and there are multiple confounders
--> Monthly Mean Article (popular press): Emerging trends in biostatistics
--> Monthly Mean Book: Structural Equation Modeling With AMOS: Basic Concepts, Applications, and Programming, Second Edition
--> Monthly Mean Definition: What is the Bonferroni correction?
--> Monthly Mean Quote: The most important figures...
--> Monthly Mean Unsung Hero Award: Thomas J. Fischbach
--> Monthly Mean Website: The NNT | Quick Summaries of Evidence-Based Medicine
--> Nick News: Nick reels in a monster fish
--> Very bad joke: The word "sustainable"...
--> Tell me what you think.
--> Join me on Facebook, LinkedIn and Twitter
--> Permission to re-use any of the material in this newsletter
--> In defense of surrogate outcomes. Surrogate endpoints have a bad reputation and this is largely deserved, but you can't ignore surrogate outcomes entirely. In the wonderful book, The Emperor of All Maladies: A Biography of Cancer by Siddhartha Mukherjee, there is a story about which cancer the first major progress was made in. It was leukemia. Leukemia was one of the worst forms of cancer and seemed like a poor candidate to tackle first. But there was one thing in leukemia's favor. You could readily detect the progress of this cancer through repeated blood draws. There was no similar way to track the progress of most solid tumors because imaging technology wasn't good enough yet. So it was only through the benefit of surrogate outcomes that any early progress against cancer could have been made.
Another defense of surrogate outcomes is described in "Impure Science: AIDS, Activism, and the Politics of Knowledge" by Steven Epstein. There were lots of controversies about the first trials of AIDS in the early 1990s, but one of the biggest controversies was about surrogate outcomes. The scientists running these trials were advocating the use of "hard" endpoints like mortality and opportunistic infections. AIDS activists, for the most part, fought against these endpoints. They were lobbying for surrogate outcomes like CD4 counts instead. One advocate had criticized the use of hard endpoints because they were the "the slowest measure of clinical improvement" and pointed out that "the drug being tested is not measured by improvements in the patients who receive it, but [opportunistic infections] or deaths in those who do not."
So why is there so much criticism of surrogate outcomes? Well, it turns out that sometimes the surrogate outcomes have misled us. The classic example is the CAST trial. CAST stands for Cardiac Arhythmia Suppression Trial. Researchers noted in the 1980s that abnormal heart rhythm problems were associated with cardiac deaths. If you could stop the rhythm problems, you could stop the deaths. It seemed like a good idea. But when anti-arrhythmic drugs were studied in a double bind randomized trial, the patients on these drugs died more often, not less often.
In general, you should look for outcomes that are directly related to things that your patients want. Such endpoints are measures of mortality, morbidity, or quality of life. An outcome measure that doesn't directly assess one of these three things is at best a surrogate for these endpoints. Treat surrogate measures with caution. But don't ignore their benefits. Surrogate outcomes will often allow you to study an intervention that could not be studied if you had to use a more concrete endpoint. The surrogate outcome can often be assessed faster and/or with less expense than a more direct outcome. The size of the effect is often more dramatic with a surrogate outcome.
Certainly you should use surrogate outcomes with caution and you should demand more direct outcomes when possible. But don't abandon surrogate outcomes entirely.
Did you like this article? Visit http://www.pmean.com/category/ClinicalImportance.html for related links and pages.
--> Data cleaning on a limited budget. Dear Professor Mean: I am currently working with a dataset that has approximately 8,000 observations. There are some observations that are more easily omitted rather than cleaning up each one. What is a good threshold for omitting values, assuming that the removed ones are random and do not have shared characteristics that might skew the data?
Well, I suppose you could say that for any data set. Data cleaning is always hard and pressing the delete key is always easy.
What you really mean to say is that data cleaning is so expensive that you don't have enough money to clean all of the data. Fair enough. Your only choice, then, is to clean some of the data (or not do the data analysis). But you want to do this in a way that is valid. Here's what you do.
First, take all of the observations that do not require cleaning. If it is not immediately obvious which data values require cleaning, then take 0 observations at this step.
Second, take a random sample of the observations that do require cleaning.
Third, clean the data in your sample. Re-combine the cleaned data set with the data set where no cleaning was needed.
Fourth, reweight the data by attaching a weight of 1.0 for the observations selected in the first step and a weight inversely proportional to the sampling probability for the observations selected in the second step. If you sample half, for example, the weight would be 2.0 because each cleaned data point counts for itself and for the corresponding dirty data point that you tossed aside. If none of the data is selected in step 1, there is no need to reweight.
This approach is valid for any sampling proportion larger than 0%, though very small sampling proportions may lead to unstable estimates. The key thing to insure unbiasedness is to not include ANY of the uncleaned data (even though some of the uncleaned data may actually be valid).
Now the question becomes, how large a sample should you take of the data needing cleaning? You might calculate what the width of the confidence interval might be at various levels of sampling and try to balance the amount of work versus the added precision.
Recall that the definition of the weighted mean is
![]()
and you can easily show that
![]()
Here's a hypothetical example. You have a Likert scale (1-5) item and for 800 of the 8,000 records, the values are either 12 or 21. All the other values look okay. Clearly the 12 and 21 represent typos and tossing these records out entirely will bias the results because the true value is almost surely 1 or 2. But finding out which requires you to dig up a large number of archived records. So select 100 of these records and check their values. Add them to the 7,200 records that are in good shape. Put a weight of 1 on the 7,200 records and a weight of 8 on the 100 records sampled from the 800 total.
How variable would this be? Well, a rough approximation is that the standard deviation is 1/4 of the range (5-1=4 for a Likert scale). If you had cleaned all 800 records, your 95% confidence interval would have had a width of plus minus 0.022. If you sample and clean 100, then the confidence interval has a width of plus/minus 0.029. That's making a conservative assumption that the cleaned variables have the same variation as the rest of the data. You can look at more extreme examples: sampling 50 would lead to a width of plus/minus 0.35, sampling 20 would lead to a width of plus minus 0.049, and sampling 10 would lead to a width of plus minus 0.065.
Did you like this article? Visit http://www.pmean.com/category/DataManagement.html for related links and pages.
--> Promoting your consulting career in the era of Web 2.0. I have been asked to develop an article of 300 to 1,200 words based on a short course I taught, "Promoting your consulting career in the era of Web 2.0." Here's an early draft that I want to share with all of you.
If you are embarking on a career as an independent statistical consultant, you have to get the word out to potential customers. There are traditional ways to do this, but there are also new ways of promoting yourself using blogs, email newsletters, and social media tools. These new approaches should not replace things like giving talks and asking current customers to recommend new client. Even so, they can be useful supplements to the things you are already doing. These new approaches are inexpensive, if not totally free, but they are labor intensive.
Among the new tools for promotion, I especially like a blog. A blog is simply a series of webpages that are presented in reverse chronological order (most recent entries at the top). Some people describe a blog as an online diary, but it doesn't have to be as personal as a diary (and many a blog) might be.
When I comment about what you should do with a blog, you should also follow that advice for Facebook, Twitter, LinkedIn, and other Web 2.0 tools. For example, a stale Facebook page, like a stale blog, is not going to attract much attention. When a particular social media alternative has special considerations, I'll try to highlight them.
Why should you start a blog instead of a website? It's a matter of your preference to a large extent, and I personally use a website for my own material. The big advantage of a blog is that it gives you very nice tools for layout, organization, and archiving. These will save you a lot of time and allow you to focus on your content.
Another attractive alternative to a blog that is somewhat "old school" is an email newsletter (like this one).
The goal of your blog (or of any other method of promoting your career) is to establish that you know your area well by giving away some of your expertise. Think of it as a free sample that will entice people to pay for more. More importantly, you want people to know you. People are very uncomfortable giving money to a total stranger. You want your blog to be a way of making an emotional connection. If your potential customers recognize you through your blog that lowers the barrier somewhat.
So what should your blog be like? Your blog should be focussed, fresh, and fun.
Focussed. Think carefully about what you will blog about. A wide ranging blog about anything and everything is likely to be too diffuse to be of interest. It will also be difficult to build up a critical mass of content when you tackle too broad a range of topics.
Focus is good, but where should you place your focus? Pick something that helps establish your credibility as an expert in a particular area, of course, but more importantly, find an under-served niche. There are 340 R bloggers, so you won't get much notice if you become the 341st blogger.
Raynauld Levesque found such a niche when he developed a website about SPSS (http://www.spsstools.net). But it wasn't a general site about SPSS, but rather a site about syntax and macros in SPSS. His site became to "go to" site for the really tough problems in SPSS that required macro solutions. Other people started contributing macros to his site. What a wonderful success you have achieved when your site gets fresh content from your readers.
Also keep your social media efforts focussed. Select one area as your primary focus and use other social media to supplement and support that primary focus. So, for example, focus mostly on a blog and use Twitter to update people when a new blog post appears. Or update people on important news events relating to statistics on Twitter, but keep an archive of these events on your webpage.
Fresh. You need to provide regular entries. It doesn't matter whether you write every other day or every other week, but make the commitment to update on a regular and predictable pattern. Don't start out too fast. You'll burn yourself out, but you'll also raise a level of expectation from your readers that you won't be able to maintain. Freshness is even more critical for social media. Old Facebook posts and old tweets fade into the background more quickly than a blog entry would. If you can't make the commitment on a particular social media site to visit and update things regularly, leave that off your list entirely rather than make a half-hearted effort.
Your blog entries can be original content, or it can be commentary on other resources. If you write your own original content, keep it short and sweet, both for your sake and for the sake of your readers. This is a free sample, and if you spend all your time on blog entries, you won't have time for your paying customers. Also, people who go looking for your content on the web aren't usually interested in a lengthy dissertation. Write enough to do the topic justice, but no more.
If you provide commentary on other resources, that is still quite valuable. It is also easy to do, but do take the time to add something more descriptive than "Hey look at this interesting website I just found." No one likes to click on a link without first getting a hint as to what they will see when they reach that site. Think of your blog entry as part of an annotated bibliography.
Twitter has a 140 character limit so you can't put any extensive original comment on it. Twitter really either serves as a conduit for brief pithy comments or links to other resources.
Fun. Make your blog fun both for you and for your readers. If it is fun for you because you chose a niche that you are passionate about, then you will have the motivation to contribute regularly. This applies double for social media. While Twitter is wildly popular, if you chafe at its 140 character limit, don't bother with Twitter. Likewise Facebook and LinkedIn have their competing partisans. Some people love the informality of Facebook and cringe at the stodgy nature of LinkedIn. Others find Facebook to be vapid and self-centered and prefer the professional demeanor of LinkedIn. Use what you're comfortable with and ignore anything else. Just because you adopt one social media tool does not mean you are obligated to recreate a similar presence on all the other social media tools.
Talk directly to your readers. You should try as much as possible to use the pronoun "you" rather than the pronoun "I" or the dreaded passive voice. Your blog is not the place to establish an aura of objectivity by adopting an encyclopedic tone.
Part of the fun of a blog is that your readers can talk back to you. When you allow readers to post comments on your blog posts, it can be scary. But these comments can add great value to your blog posts. Your readers will highlight areas that they like or define controversies when they point out things they don't like. You will also get readers who feel a better emotional connection to you. Stay vigilant and remove off-topic or off-color responses. Social media offers you more control over readers comments
How much self-promotion can/should you do? While some self-promotion is okay, it's a fine line. You don't want to act like the stereotypical insurance salespeople who are constantly badgering all of their friends to buy more insurance. A good ratio to start at is one blog post directly promoting your consulting career for every ten blog posts that do not.
Be even more cautious about self-promotion on social media sites. These sites often evolve community standards about what is acceptable and what is not and these vary greatly across different social media sites. Even within a social media site there is substantial variation on what constitutes excessive self-promotion. The best thing to to is to watch how others behave and emulate them. If someone complains, apologize profusely and publicly. The worst thing you can do is argue, even if the complaint is unfounded. Let others in the community come to your defense if someone tries to enforce a standard more rigid that what the community as a whole prefers.
Social media does have an advantage over a blog in that if you push too hard on self-promotion, you will get immediate feedback through befriending, loss of followers, etc. On the positive side, the success of your Twitter feeds can easily be measured by the number of times you get retweeted and the success of your Facebook posts is shown by the number of "likes" that you get.
In summary, blogs and social media tools shouldn't replace more traditional means of promotion, but they can help with name recognition. If you use blogs and social media, be sure that you make your content focussed, fresh, and fun.
Did you like this article? Visit http://www.pmean.com/category/HumanSideStatistics.html for related links and pages.
--> Monthly Mean Article (peer reviewed): M Soledad Cepeda, Ray Boston, John T Farrar, Brian L Strom. Comparison of logistic regression versus propensity score when the number of events is low and there are multiple confounders. Am. J. Epidemiol. 2003;158(3):280-287. Abstract: "The aim of this study was to use Monte Carlo simulations to compare logistic regression with propensity scores in terms of bias, precision, empirical coverage probability, empirical power, and robustness when the number of events is low relative to the number of confounders. The authors simulated a cohort study and performed 252,480 trials. In the logistic regression, the bias decreased as the number of events per confounder increased. In the propensity score, the bias decreased as the strength of the association of the exposure with the outcome increased. Propensity scores produced estimates that were less biased, more robust, and more precise than the logistic regression estimates when there were seven or fewer events per confounder. The logistic regression empirical coverage probability increased as the number of events per confounder increased. The propensity score empirical coverage probability decreased after eight or more events per confounder. Overall, the propensity score exhibited more empirical power than logistic regression. Propensity scores are a good alternative to control for imbalances when there are seven or fewer events per confounder; however, empirical power could range from 35% to 60%. Logistic regression is the technique of choice when there are at least eight events per confounder." [Accessed on March 21, 2012]. http://www.ncbi.nlm.nih.gov/pubmed/12882951.
Did you like this article? Visit http://www.pmean.com/category/CovariateAdjustment.html for related links and pages.
--> Monthly Mean Article (popular press): Emerging trends in biostatistics, Marie Davidian, Cutting Edge, March 16, 2012. Excerpt: "Almost daily, the media reports another health-related discovery. A study in a leading medical journal finds an association between certain genetic variants and increased risk of heart disease. Another suggests rethinking how bone density testing is used to diagnose and treat osteoporosis. A clinical trial shows no evidence that a new anti-platelet therapy reduces the incidence of death or serious health outcomes relative to an existing treatment in coronary artery disease patients. Three major studies suggest that exposure to air pollution may be implicated in stroke or cognitive decline. Behind all of these findings? Biostatistics - the science of development of statistical theory and methods for application to data-driven challenges in the health and biological sciences."http://membercentral.aaas.org/articles/emerging-trends-biostatistics
Did you like this article? Visit http://www.pmean.com/category/TeachingResources.html for related links and pages.
--> Monthly Mean Book: Barbara M. Byrne, Structural Equation Modeling With AMOS: Basic Concepts, Applications, and Programming, Second Edition. Description: This book is a very easy introduction to SEM for those new to the area. It uses AMOS software for all of its examples.
Did you like this book? Visit http://www.pmean.com/category/UnusualData.html for related links and pages.
--> Monthly Mean Definition: What is the Bonferroni correction? The Bonferroni correction is a statistical adjustment for the multiple comparisons. It effectively raises the standard of proof needed when a scientist looks at a wide range of hypotheses simultaneously. There are two common sources of multiple hypotheses. First, you might be interested in looking at multiple outcome measures. You have an exposure that you think might cause cancer and you think that exposure might be associated with bladder cancer, brain cancer, colon cancer, liver cancer, lung cancer, ovarian cancer, prostate cancer, skin cancer, and "that funny little thing hanging in the back of your throat" cancer.
The Bonferroni correction is quite simple. If we are testing n outcomes instead of a single outcome, we divide our alpha level by n. Suppose we were looking at the association of sodium chloride and 8 different types of cancers. Instead of testing at the tradition .05 alpha level, we would test at alpha=.05/8=.00625 level. This would ensure that the overall chance of making a Type I error is still less than .05.
You can also apply the Bonferroni correction by adjusting the p-value. A Bonferroni adjusted p-value would just be the normal p-value multiplied by the number of outcomes being tested. If the adjusted p-value ended up greater than 1.0, it would be rounded down to 1.0. Suppose the 20 p-values before Bonferrroni adjustment are 0.001, 0.002, 0.005, 0.01. 0.04, 0.1, 0.3, and 0.7. Multiply each of these by 8 (and round anything over 1.0 down to 1.0). This gives you Bonferroni adjusted p-values of 0.008, 0.016, 0.04, 0.08, 0.32, 0.80, 1.0, and 1.0.
Some scientists dislike the use of the Bonferroni correction; they prefer instead that researchers clearly label any results as preliminary and/or exploratory. Furthermore, the Bonferroni correction can cause a substantial loss in the precision of your research findings.
Your general perspective on hypothesis testing is important. One perspective that clearly calls for a Bonferroni adjustment is a global null hypothesis. Suppose that you are measuring a large number of outcome variables, and you will conclude that a treatment is effective (or that an exposure is dangerous) if you find a statistically significant effect on ANY ONE one of your outcome variables. So a new drug for asthma would be considered effective if it reduced the number of symptoms as measured by the number of wheezing episodes OR the number of emergency room visits related to asthma OR the number of patients who no longer required steroid treatment OR if the average patient had an improvement in lung capacity as measured by FEV1 OR as measured by the FVC vale OR as measured by the FEV1/FVC ratio OR as measured by the FEF25-75 value OR as measured by the PEFR value OR if the average patient had a better quality of life as measured by the SF-36. When there is a clear global null hypothesis, then you should use a Bonferroni adjustment.
Consider a restrictive hypothesis, a conceptual hypothesis at the other extreme. Suppose that you will consider a treatment as effective only if it shows a statistically significant improvement in all of those outcome variables. With a restrictive hypothesis, you might be justified in increasing your alpha level to .10 or .15 since your criteria for success is so stringent. In truth most studies do not gravitate to either extreme, making it difficult for you to decide whether to use the Bonferroni adjustment.
When you need to examine many different outcome measures in a single research study, you still may be able to keep a narrow focus by specifying a small number of your outcome measures as primary variables. Typically, a researcher might specify 3-5 variables as primary. The fewer primary outcome variables, the better.
You would then label as secondary those variables not identified as primary outcome variables. When you designate a small number of primary variables, you are making an implicit decision. The success or failure of your intervention will be judged almost entirely by the primary variables. If you find that none of the primary variables are statistically significant, then you will conclude that the intervention was not successful. You would still discuss any significant findings among your secondary outcome variables, but these findings would be considered tentative and would require replication.
When some but not all of your outcome measures reach statistical significance, you should examine them for consistency with known mechanisms. In a study of male reproductive toxicology, some outcome measures are related to hormonal disruptions, others to incomplete sperm maturation, and still others to problems with the accessory sex glands. If the significant outcome variables all can be tied to a common mechanism, you have greater confidence in the research results. On the other hand, if each significant variable requires a different mechanistic explanation, you have less confidence. Also, if one outcome associated with a certain mechanism is significant and other outcomes associated with the same mechanism are not even approaching borderline significance, then you have less confidence in your findings.
Another area where the Bonferroni correction becomes useful is with comparisons across multiple groups of subjects. If you have four treatment groups (e.g., A, B, C, and D), then there are six possible pairwise comparisons among these groups (A vs B, A vs C, A vs D, B vs C, B vs D, C vs D). If you are interested in all possible pairwise comparisons, the Bonferroni correction provides a simple way to ensure that making these comparisons does not lead to some of the same problems as testing multiple outcome measures. There are other approaches that work more efficiently than Bonferroni. Tukey's Honestly Significant Difference is the approach I prefer. But you also need to be sure that you are truly interested in ALL possible pairwise comparisons.
Although all of the emphasis on this page has been on statistical significance, you should always evaluate practical significance as well. Suppose that among all your outcome measures, none shows an effect large enough to have any practical or clinical impact. In such a situation, discussion of whether to use a Bonferroni adjustment becomes meaningless.
Too many studies have an inadequate sample size, and the Bonferroni correction will make this problem even worse. If you apply a Bonferroni correction with a data set that is already too small, you are implicitly stating that it is important only to control the probability of a Type I error (rejecting the null hypothesis when the null hypothesis is true), and that you don't care about limiting the probability of a Type II error (accepting the null hypothesis when the null hypothesis is false).
Examples: In a study of Parkinson's disease (Kaasinen 2001), a group of 61 unmedicated Parkinson's disease patients and 45 healthy controls were compared on 22 separate personality scales. The was prior data to suggest that novelty seeking would be lower in patients with Parkinson's, so this comparison was made without any Bonferroni adjustments. The remaining personality scores, however, had no such prior information and a Bonferroni adjustment was used for these remaining scales. An additional analysis looked PET scans for a subset of 47 Parkinson's patients. The 18F-dopa uptake in 10 regions of the brain were correlated with the 22 personality traits. The correlations involving novelty seeking were not adjusted, but the remaining correlations were adjusted to account for the fact that 210 (10x21) correlations were being analyzed. A significant correlation was observed between harm avoidance and 18F-dopa uptake in the right caudate nucleus (r=0.53, corrected P = 0.04). Interestingly, there was not a statistically significant correlation in the left caudate nucleus (r=0.43, corrected P=0.88) even though the uncorrected p-value was less than 0.01.
In a study of intraoperative hypothermia (Janicki 2002), 12 patients were randomized to a forced air warming system and 12 to a newly developed whole body water garment. The primary outcome, body core temperature, was measured at five times during the operation (incision; 1 hr after incision; placement of liver graft into the recipient; reperfusion; and closing) and at three times after the operation (T=0, 1, or 2 hours in the ICU). The comparisons were adjusted by dividing the alpha level by 5 (for the intraoperative measures) or by 3 (for the postoperative measures). It would have been possible to perform a single Bonferroni correction across all eight measures; perhaps the authors felt that intraoperative and postoperative measurement represented distinct and separate comparisons.
V Kaasinen, E Nurmi, J Bergman, O Eskola, O Solin, P Sonninen, J O Rinne. Personality traits and brain dopaminergic function in Parkinson's disease Proc. Natl. Acad. Sci. U.S.A. 2001;98(23):13272–13277. [Accessed on March 3, 2012]. http://www.ncbi.nlm.nih.gov/pubmed/11687621.
Piotr K Janicki, Cristina Stoica, William C Chapman, J Kelly Wright, Garry Walker, Ram Pai, Ann Walia, Mias Pretorius, C Wright Pinson. Water warming garment versus forced air warming system in prevention of intraoperative hypothermia during liver transplantation: a randomized controlled trial [ISRCTN32154832] BMC Anesthesiol. 2002;2(1):7. [Accessed on March 3, 2012]. http://www.ncbi.nlm.nih.gov/pubmed/12441007.
Did you like this article? Visit http://www.pmean.com/category/MultipleComparisons.html for related links and pages.
--> Monthly Mean Quote: The most important figures that one needs for management are unknown or unknowable, W. Edwards Deming as quoted at curiouscat.com/deming/managewhatyoucantmeasure.cfm. Note that this quote is frequently misinterpreted. Click on this link for an interesting perspective.
--> Monthly Mean Unsung Hero Award: Thomas J. Fischbach. I just learned of the death of a colleague, Thomas J. Fischbach, who I worked with while I was at the National Institute for Occupational Safety and Health (NIOSH), part of the Centers for Disease Control and Prevention (CDC). He worked in a different division, so our paths did not cross too often. But I was always impressed with his diligence. He worked largely with chemists at NIOSH and understood many of the subtleties that made analysis of this data different from other types of data.
There's a tendency among many in the United States to sneer at the federal bureaucracy. While I won't deny that there aren't problems, I have to point out that characterizing problems with the bureaucracy should never be personalized to the people who work inside the federal government. Tom personified many of the characteristics of the federal workers that I had the privilege of working with while I was at NIOSH. He was hard working, dedicated, and devoted to the mission of NIOSH. Tom retired shortly after I left NIOSH, and I only heard a few updates from some of his colleagues.
There was an email sent through the CDC system that was forwarded to me, that paid a touching tribute to Tom. I am reproducing most of it here.
With great sadness we announce the death of Thomas J. Fischbach, colleague, mentor, friend, statistician, and family man who passed away on Thursday, March 22, 2012, after a brief illness. He was a kind and hospitable man who will be missed.
Tom was born on December 23, 1934 and grew up in South Dakota, where he attended South Dakota State University. Later he served as a platoon leader in the U.S. army, after which he earned a master's degree in statistics from the University of Wisconsin, Madison. Before coming to the National Institute for Occupational Safety and Health (NIOSH) as a commissioned officer in 1977 he worked for the University of Wisconsin and for the Wisconsin Regional Medical program.
Tom was a careful thinker who sought out important problems and who did not refrain from dealing with controversial issues. Tom was able to defend a position strongly in the face of unfounded opposition. At NIOSH, his significant contributions included: work on analysis of worker disability data, work with NIOSH engineers to control dangerous workplace hazards (enhancing the life of factory and construction workers), methodology for evaluation of analytical methods and their accuracy, time series data analysis for real-time instruments, and promotion of the use of measurements below the limit of detection (LOD) in statistical analyses. These are all important areas of continuing research, which still owes a great deal to Tom's skill and integrity. Aside from applications, Tom had a deep understanding and interest in the fundamentals of statistics. He also had considerable wit: a non-statistician in the audience at his LOD presentation stated that she had never heard such an entertaining presentation from a statistician! He was also a mentor for younger researchers. Tom fought hard for the ideas and the people in whom he believed. He retired in February, 1997.
Tom was a man of many interests: lover of opera, real-estate owner, and lover of the out-of-doors. He and his beloved wife, Alice, retired to a 98 acre wooded area in Indiana, where he planted trees and also perfected his maple syrup.
Tom was a devoted husband, father, grandfather, great-grandfather, brother, son, and nephew. He and Alice hosted and visited their large family, with distance never an obstacle.
--> Monthly Mean Website: Jarone Lee, Mukherjee Koustav, Joshua Quaas, Daniel Runde, Ashley Shreves, Graham Walker. The NNT | Quick Summaries of Evidence-Based Medicine. Excerpt: "The Number Needed to Treat (NNT) is a powerful tool to communicate benefit and harm that both patients and doctors can understand. Click to briefly learn more about the NNT and why it's so great." [Accessed on April 11, 2012]. http://www.thennt.com/.
Did you like this website? Visit http://www.pmean.com/category/MeasuringBenefitRisk.html for related links and pages.
--> Nick News: Nick reels in a monster fish. I am not a fisher and I have no desire to become one. Nick, on the other hand, loves to fish, and that's why being in Cub Scouts is good for him. Our Cub Scout pack has several events with fishing instruction and opportunities to land a big one. This past weekend, we were at Miami State Fishing Lake for a campout, and Nick hit the jackpot.
![[[Nick with a large mouth bass]]](images/201203/nick01.jpg)
Here's a picture of him with a large mouth bass. As you can see, this fish is huge and has earned its name. That fish looks like it could swallow you whole and take you to Nineveh. But that wasn't all.
![[[Nick with a second large mouth bass]]](images/201203/nick02.jpg)
Here's a second fish he caught, even bigger than the first. He says he caught six fish total on that trip, but I can only vouch for these two.
Later that same day, he caught the inevitable "weedfish."
--> Very bad joke: The word "sustainable"...
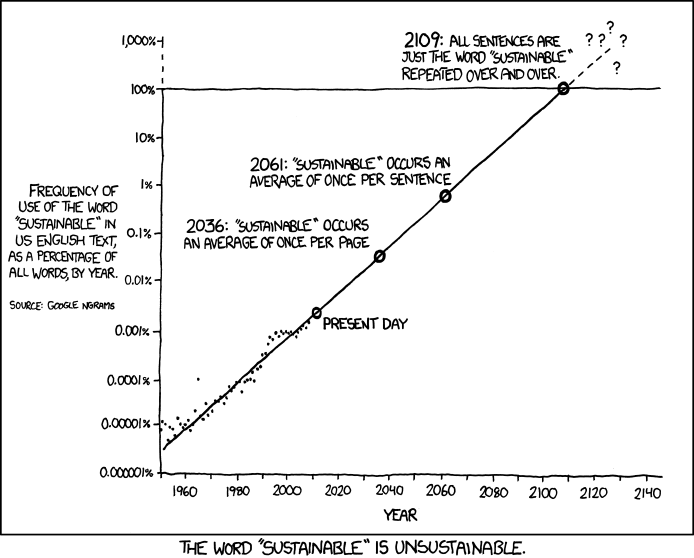
This comic strip was drawn by Randall Munroe and is available under an open source license. You can find the original cartoon at
-->
http://xkcd.com/1007/
--> Tell me what you think. How did you like this newsletter? Give me some feedback by responding to this email. Unlike most newsletters where your reply goes to the bottomless bit bucket, a reply to this newsletter goes back to my main email account. Comment on anything you like but I am especially interested in answers to the following three
questions.
--> What was the most important thing that you learned in this newsletter?
--> What was the one thing that you found confusing or difficult to follow?
--> What other topics would you like to see covered in a future newsletter?
I received feedback from four people. Three people liked the section on quasi-experimental alternatives to randomization, and one mentioned the article at their site
--> http://www.delfini.org/delfiniClick_PrimaryStudies.htm#quasirand
Another reader wanted to chat about social media. I haven't had a chance to follow-up on that but note my second article in this month's newsletter. I also got a comment that Nick is adorable. He's adopted, so I can't claim that he inherited his good looks from me. But thanks.
--> Join me on Facebook, LinkedIn, and Twitter. I'm just getting started with social media. My Facebook page is www.facebook.com/pmean, my page on LinkedIn is www.linkedin.com/in/pmean, and my Twitter feed name is @profmean. If you'd like to be a Facebook friend, LinkedIn connection (my email is mail (at) pmean (dot) com), or tweet follower, I'd love to add you. If you have suggestions on how I could use these social media better, please let me know.
--> Permission to re-use any of the material in this newsletter. This newsletter is published under the Creative Commons Attribution 3.0 United States License, http://creativecommons.org/licenses/by/3.0/us/. You are free to re-use any of this material, as long as you acknowledge the original source. A link to or a mention of my main website, www.pmean.com, is sufficient attribution. If your re-use of my material is at a publicly accessible webpage, it would be nice to hear about that link, but this is optional.
What now?
Sign up for the Monthly Mean newsletter
Review the archive of Monthly Mean newsletters
![]() This work is licensed under a
Creative
Commons Attribution 3.0 United States License.
This work is licensed under a
Creative
Commons Attribution 3.0 United States License.