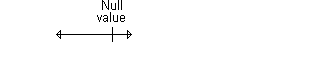
This page has moved to my new website.
Dear Professor Mean: Can you give me a simple explanation of what a confidence interval is?
We statisticians have a habit of hedging our bets. We always insert qualifiers into our reports, warn about all sorts of assumptions, and never admit to anything more extreme than probable. There's a famous saying: "Statistics means never having to say you're certain."
We qualify our statements, of course, because we are always dealing with imperfect information. In particular, we are often asked to make statements about a population (a large group of subjects) using information from a sample (a small, but carefully selected subset of this population). No matter how carefully this sample is selected to be a fair and unbiased representation of the population, relying on information from a sample will always lead to some level of uncertainty.
I'll show some of the formulas and calculations below, but here are some spreadsheets that I commonly use to make simple confidence interval calculations.
Short Explanation
A confidence interval is a range of values that tries to quantify this uncertainty. Consider it as a range of plausible values. A narrow confidence interval implies high precision; we can specify plausible values to within a tiny range. A wide interval implies poor precision; we can only specify plausible values to a broad and uninformative range.
Consider a recent study of homoeopathic treatment of pain and swelling after oral surgery (Lokken 1995). When examining swelling 3 days after the operation, they showed that homoeopathy led to 1 mm less swelling on average. The 95% confidence interval, however, ranged from -5.5 to 7.5 mm. From what little I know about oral surgery, this appears to be a very wide interval. This interval implies that neither a large improvement due to homoeopathy nor a large decrement could be ruled out.
Generally when a confidence interval is very wide like this one, it is an indication of an inadequate sample size, an issue that the authors mention in the discussion section of this paper.
How to Interpret a Confidence Interval
When you see a confidence interval in a published medical report, you should look for two things. First, does the interval contain a value that implies no change or no effect? For example, with a confidence interval for a difference look to see whether that interval includes zero. With a confidence interval for a ratio, look to see whether that interval contains one.
Here's an example of a confidence interval that contains the null value. The interval shown below implies no statistically significant change.
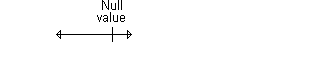
Here's an example of a confidence interval that excludes the null value. If we assume that larger implies better, then the interval shown below would imply a statistically significant improvement.
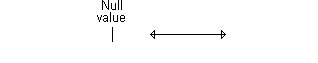
Here's a different example of a confidence interval that excludes the null value. The interval shown below implies a statistically significant decline.

Practical Significance
You should also see whether the confidence interval lies partly or entirely within a range of clinical indifference. Clinical indifference represents values of such a trivial size that you would not want to change your current practice. For example, you would not recommend a special diet that showed a one year weight loss of only five pounds. You would not order a diagnostic test that had a predictive value of less than 50%.
Clinical indifference is a medical judgement, and not a statistical judgement. It depends on your knowledge of the range of possible treatments, their costs, and their side effects. As statistician, I can only speculate on what a range of clinical indifference is. I do want to emphasize, however, that if a confidence interval is contained entirely within your range of clinical indifference, then you have clear and convincing evidence to keep doing things the same way (see below).

One the other hand, if part of the confidence interval lies outside the range of clinical indifference, then you should consider the possibility that the sample size is too small (see below).

Some studies have sample sizes that are so large that even trivial differences are declared statistically significant. If your confidence interval excludes the null value but still lies entirely within the range of clinical indifference, then you have a result with statistical significance, but no practical significance (see below).

Finally, if your confidence interval excludes the null value and lies outside the range of clinical indifference, then you have both statistical and practical significance (see below).

The Standard Error
In many situations, the width of a confidence interval is proportional to the standard error. The standard error is defined the variability for a statistical estimate. You can compute a crude confidence interval by taking the estimate plus or minus twice the standard error.
Confidence Interval for a Simple Average
There are lots of different formulas for the confidence interval and the standard error, depending on the context of the problem. The simplest formula appears when you estimate an average from a single sample. In this situation, the standard error would be
![]()
where sigma represents the variability of the original data and n represents the size of the sample. The crude confidence interval would be the sample mean plus or minus two standard errors.
The width of your confidence interval goes down as the sample size goes up, since you are placing a larger value in the denominator. This is a classic and intuitive relationship in statistics: larger sample sizes provide greater precision (that is, narrower confidence intervals).
One way of planning a sample size for your study is to try to make sure your confidence interval has an adequate amount of precision. Although larger sample sizes mean narrower confidence intervals, there is usually a point of diminishing returns. This occurs when further shrinking of the interval is not worth the cost of additional subjects.
An often overlooked strategy for gaining precision is by finding a way to shrink sigma, the variability in your original data set. For example, use of calibration and quality control checks in a laboratory can often provide substantially smaller values for sigma.
I have a spreadsheet that calculates confidence intervals for a simple average:
Confidence Interval for a Difference Between Two Averages
If we were interested in estimating the difference in averages between two independent samples of data, the standard error of the estimated difference would be
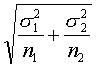
where the subscripts 1 and 2 indicate whether the values come from the first or the second group. Notice that the standard error and hence the width of the confidence interval goes down as either or both sample sizes go up.
When you are planning a research study comparing two groups, it is often helpful to consider different allocations of samples to the two groups. For example, if your first group is much more variable than the second group, you might be better off trying for a larger sample size in that group, rather than trying to get equal numbers in each group.
I have a spreadsheet that calculates the confidence interval for the difference between two averages:
Confidence Interval for a Proportion
If we compute a proportion, p, from a sample, the standard error of that proportion would be
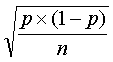
Just like the previous examples, larger sample sizes lead to smaller standard errors and narrower confidence intervals.
Did you notice in this formula that the width of the confidence interval is related to the estimate itself. A bit of work with calculus will show you that, assuming the sample size stays the same, the widest confidence interval occurs when p=0.5. Both rarer and more frequent events than 50% will produce narrower intervals.
Here is a simple spreadsheet that will calculate the confidence interval for a proportion.
Confidence Interval for an Odds Ratio
The final example involves computing an odds ratio. We often use the odds ratio to summarize data in a two by two table. The rows of the table might represent disease status (healthy/diseased) and the columns might represent exposure status (exposed/unexposed). In this case, the odds ratio would represent the relative change in the odds of disease between exposed and unexposed patients.
Or possibly the rows might represent treatment status (active drug/placebo) and the columns might represent health outcome (improvement/no improvement). Here, the odds ratio represents the relative change in the odds of improvement between drug and placebo.
If we let the letters a, b, c, and d represent the frequency counts in a two by two table (see below)
![]()
then the odds ratio would be ad/bc. The odds ratio is skewed, so we cannot easily compute a standard error for the odds ratio itself. We can, however, find a standard error for the natural logarithm of the odds ratio. It is simply
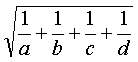
We see that as any or all of the counts in the two by two table increase, the confidence interval for the log odds ratio shrinks. Also, it turns out that the smallest count in the two by two table plays the largest role in determining the size of the standard error.
Confidence interval for a Rate Ratio
[[Details to be provided soon.]]
Confidence interval for a Relative Risk
[[Details to be provided soon.]]
Confidence interval for a Correlation
[[Details to be provided soon.]]
Example of a Confidence Interval For a Mean
In a study of immunotherapy in children with asthma, 61 patients showed an average improvement of 2.5% peak expiratory flow rate with a standard deviation of 11%. We divide the standard deviation by the square root of 61 to get a standard error of 1.4. A crude confidence interval would be 2.5% plus or minus 2.8% which equals 0.3% to 4.8%. I'm not an expert of asthma, but if we defined a range of clinical indifference to be an improvement of less than 5%, then this confidence interval is entirely within the range of clinical indifference.
Example of a Confidence Interval for An Odds Ratio
In the same study, the author noted that 15 out of 53 immunotherapy patients showed partial remission on their need for medication. This sample size is smaller because of a small number of dropouts. In the placebo group, 12 out of 57 showed partial remission. The two by two table for these data looks like
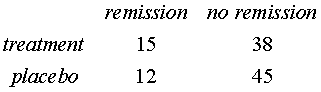
The odds ratio is 1.5, which shows that the immunotherapy treatment increases the odds of partial remission. The natural log of the odds ratio is 0.6. For this calculation, be sure that you use a natural logarithm and not a base 10 logarithm.
The standard error of the log odds ratio is
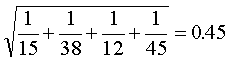
So a crude confidence interval for the log odds ratio is 0.6 plus or minus 0.9 which equals -0.5 to 1.3. We can exponentiate (use the exp button on your scientific calculator) to convert back to the original measurement scale. This gives us a confidence interval of 0.6 to 3.6 for the odds ratio itself. Even though this interval contains 1, we still have to allow for the possibility that the improvement might be as large as two-fold or three-fold.
Confidence interval for the difference compared to two separate confidence intervals
It's important to avoid comparing two separate confidence intervals to see if they overlap. Someone brought me data where the proportion of patients who tested positive was 41.6% (n=202) for the first group and 50.7% (n=802) in the second group. The individual confidence intervals are (34.8% to 48.4%) and (47.2% to 54.2%). Notice that the two intervals overlap, but just barely. The confidence interval for the difference in two proportions, however, is (-16.7% to -1.5%) which provides evidence that the two proportions differ. This is a borderline result, of course, since one side of the interval almost reaches zero.
The reason that you can have overlap in the individual intervals is that you don't add the two standard errors together. The standard error for the two individual intervals would be
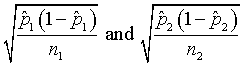
and the standard error for the difference is
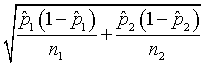
You can compare these calculations by using the spreadsheet
and comparing the result to the spreadsheet that computes a confidence interval for a single proportion:
These are not very sophisticated spreadsheets and they use the simplest formulas available. The nice thing, though, about these spreadsheets is that they allow you to play a bunch of "what if" games.
Exact confidence intervals
Some alternate confidence intervals based on the exact binomial distribution will provide better results than my spreadsheet, which uses the normal approximation to the binomial distribution. You can get such an interval using StatXact software, produced by Cytel, Inc. A paper (PDF format) at the their web site discusses some of these exact procedures and how to get p-values from an exact confidence interval.
Confidence intervals for complex research designs
Someone asked me by email about confidence intervals in complex research designs. This person had rejected the use of post hoc power calculations, and wanted instead to use confidence intervals to help answer the question about whether the sample size was adequate. In a simple setting, such as the comparison of a treatment group to a control group, the choice of confidence interval is obvious, but how would you handle complex research designs (more than two groups and/or repeated measurements over time).
For example, if you are comparing a low, medium, and high dose to a placebo, then three confidence intervals for the difference between each dose and placebo might be interesting. If there is no dose response pattern, then a confidence interval comparing the two extreme doses might be helpful because it places limits on the size of any possible dose response pattern.
If your repeated measures include a baseline, 6 month and 12 month measures, then a confidence interval for the short term change (6 month minus baseline) and an interval for the long term change (12 month minus baseline) might be useful. Combining the two scenarios together, perhaps you know there is a strong placebo response, so then you might want a confidence interval for the long term change score between each dose and the placebo.
If you end up with more than two or three confidence intervals, you might want to consider some sort of adjustment like Bonferroni.
Other pages that compute confidence intervals
There are lots of web pages out there that do confidence interval calculations, using Java or JavaScript. Here are a few nice examples of confidence intervals for a single proportion:
Exact Binomial and Poisson Confidence Intervals, John C. Pezzullo. members.aol.com/johnp71/confint.html
The Confidence Interval of a Proportion, Richard Lowry. faculty.vassar.edu/lowry/prop1.html
Confidence interval of a proportion or count, GraphPad. www.graphpad.com/quickcalcs/ConfInterval1.cfm
Large Sample Confidence Interval for a Proportion Applet, James W. Hardin. stat.tamu.edu/~jhardin/applets/signed/case6.html
and for the difference between two proportions:
The Confidence Interval for the Difference Between Two Independent Proportions, Richard Lowry. faculty.vassar.edu/lowry/prop2_ind.html
A nice general reference for web pages that do statistical calculations is
Web Pages that Perform Statistical Calculations. Pezzullo JC. Accessed on 2004-07-08. members.aol.com/johnp71/javastat.html
Summary
A confidence interval is a range of plausible values that accounts for uncertainty in a statistical estimate.. A narrow confidence interval implies high precision; a wide interval implies poor precision.
When you see a confidence interval in a published medical report, you should look for two things.
Further Reading