P.Mean: (created 2013-). News: Sign up for "The Monthly Mean," the newsletter that dares to call itself average, www.pmean.com/news.

I ran across a Facebook posting that immediately struck me as ludicrous.

The first thing you'll notice is that the posting is wrong. If you look at the calendar
--> http://www.timeanddate.com/calendar/
you'll see that December has five Sundays, Mondays, and Tuesdays. The posting was stale, apparently.
--> http://www.timeanddate.com/calendar/?year=2012&country=1
does indeed have five Mondays, Saturdays, and Sundays. But is this really something that occurs only once every 823 years? There are seven possible calendars for December, depending on whether December 1 occurs on a Sunday,

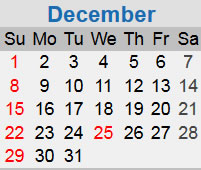
or a Monday,

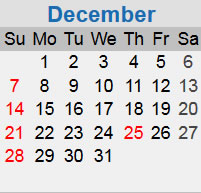
or a Tuesday,

or a Wednesday,

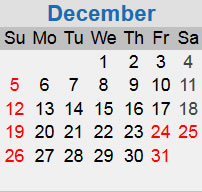
or a Thursday,

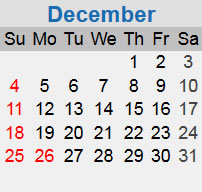
or a Friday,

or a Saturday,

It will help later to label each of these calendars with a number. Let's call the Sunday calendar 0, the Monday calendar 1, the Tuesday calenar 2, and so forth through the Saturday calendar which will be 6. You can think of these labels as the number of blanks at the beginning of the first row.

With only seven possible calendars, it would seem rather surprising that one of the them would occur only once every 823 years. You can understand the sequence of calendars using modular arithmetic.

Modular arithmetic involves calculation of the remainder only from a division problem. So 20 mod 3 would equal 2 because when you divide 20 by 3 you get 6 with a remainder of 2. Some other examples of modular arithmetic

13 mod 2 = 1

29 mod 5 = 4

44 mod 4 = 0

Modular arithmetic produces a 0 only when the first number is evenly divisible by the second number.

The key result from the calendar perspective is that

365 mod 7 = 1

This reflects the fact that there are not 52 weeks in a year, but 52 weeks plus a day. What that means is that every year, the calendar jumps forwards by a day. The December calendar starts on a Sunday this year, and will start on a Monday next year, and on a Tuesday in 2015.

This also works for any other day in the year. My wife's birthday was on a Thursday this year, will be on a Friday next year, and on a Saturday in 2015. Our anniversary was on a Saturday this year, will be on a Sunday next year, and a Monday in 2015. Check it out with your birthday or anniversary.

So, it looks like the calendars will repeat themselves every seven years. Well, not quite. There is a leap year every fourth year, and that makes things a tiny bit more complicated. In a leap year, a day skips ahead by 2 because

366 mod 7 = 2

The skip 2 pattern occurs in the leap year itself for March 1 and later. For January and February dates, the skip 2 pattern occurs the year after the leap year. So for any given year, a date will hop ahead by one or two days, depending on whether a leap year is involved. So my wife's birthday will cycle Thursday, Friday, Saturday, Monday (+2 because of the leap year), Tuesday, Wednesday, Thursday, Saturday (+2 again because of the leap year), and so forth. Did you notice that Sunday did not appear on that list? We'll see that a Sunday birthday has to be in the cards, though, because even though the calendar doesn't jump forward with perfect regularity, it has to cycle every 28 years.

A four year period has 1,461 days (3*365+366). Using modular arithmetic, notice that

1,461 mod 7 = 5

That means that the day jumps ahead by five every fourth year. You could have figured it out by noting that it would jump ahead 3 days on the 3 non-leap years and 2 more days on the leap year. So my anniversary jumps from Saturday in 2013 up ahead five days to Thursday in 2017. Then it jumps to Tuesday in 2021, Sunday in 2025, Friday in 2029, Wednesday in 2033, Monday in 2037, and Saturday again in 2041. Let's list those values in a table

2013 Sa (6)
2017 Th (4)
2021 Tu (2)
2025 Su (0)
2029 Fr (5)
2033 We (3)
2037 Mo (1)
2041 Sa (6)

Notice that I numbered the days with Sunday=0 through Saturday=6. The list has a pattern, and you can replicate the pattern using modular arithmetic again.

(6+5) mod 7 = 4
(4+5) mod 7 = 2
(2+5) mod 7 = 0
(0+5) mod 7 = 5
(5+5) mod 7 = 3
(3+5) mod 7 = 1
(1+5) mod 7 = 6

The repeated cycle occurs, in part, because 7 does not divide evenly into 365, 366, or 1461. The take home message is that the calendar appears somewhat irregular to us, and with good reason. Even with all the irregularities, though, the calendar is guaranteed to repeat every 28 years. If you want proof of this, look at the 2012 calendar, with the so-called "moneybags" month in December.

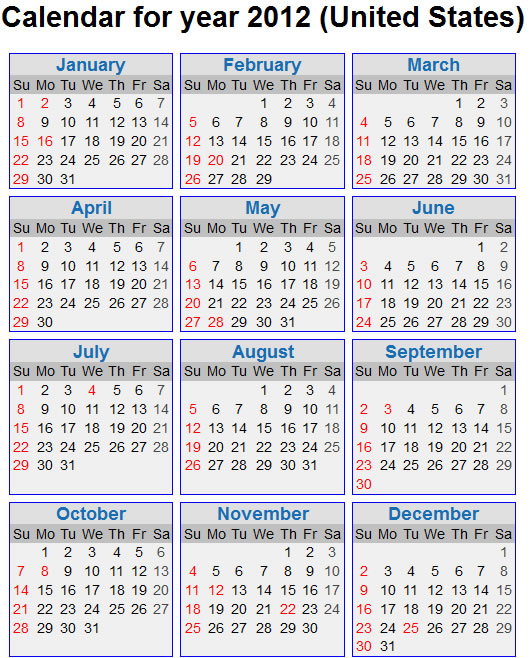
Now look at the calendar for 28 years earlier, 1984.

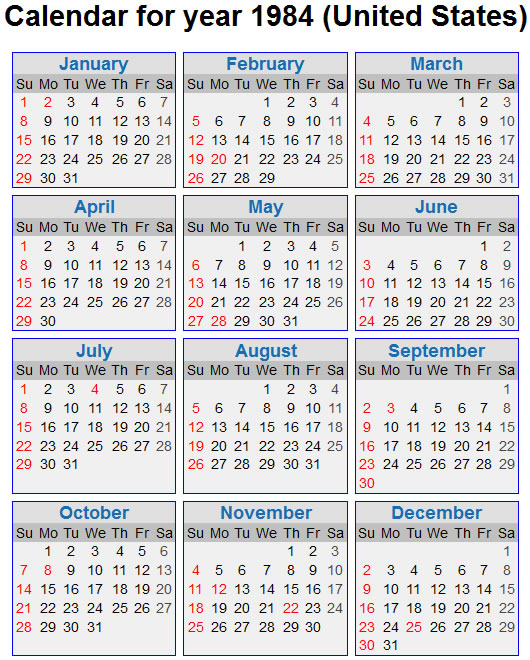
There are some irregularly spaced repetitions between 1984 and 2012, but you can guarantee a repetition every 28 years, just like clockwork.

For more information about the preposterous 823 year "moneybags" claim, see
--> http://www.snopes.com/inboxer/trivia/fivedays.asp

This page was written by Steve Simon and is licensed under the Creative Commons Attribution 3.0 United States License. Need more information? I have a page with general help resources. You can also browse for pages similar to this one at Incomplete pages.