P.Mean: Statistical distributions borrowed from Wikipedia (created 2012-05-02)

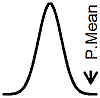
P.Mean: Statistical distributions borrowed from Wikipedia (created 2012-05-02).

News: Sign up for "The Monthly Mean," the newsletter that dares to call itself average, www.pmean.com/news.

I am finding that I need to refer often to various statistical distributions on Wikipedia. Since Wikipedia is open source, I can re-use their content here. So here are some of my favorite statistical distributions.

Beta distribution.

Beta distribution

Some composite distributions involving the beta distribution are

Beta negative binomial distribution.

Beta binomial distribution.

A closely related distribution is Inverse beta distribution.

There is an application where I needed the moment generating function of the beta distribution. Here it is.

$1 +\sum_{k=1}^{\infty} \left( \prod_{r=0}^{k-1} \frac{\alpha+r}{\alpha+\beta+r} \right) \frac{t^k}{k!}$

Binomial distribution.

Binomial distribution

Chi-square distribution.

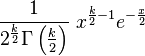
$\frac{1}{2^{\frac{k}{2}}\Gamma\left(\frac{k}{2}\right)}\; x^{\frac{k}{2}-1} e^{-\frac{x}{2}}\,$

A closely related distribution is the noncentral chi-square distribution.

$\frac{1}{2}e^{-(x+\lambda)/2}\left (\frac{x}{\lambda} \right)^{k/4-1/2} I_{k/2-1}(\sqrt{\lambda x})$

Exponential distribution.

This distribution has two forms.

Exponential distribution

F distribution.

$\frac{\sqrt{\frac{(d_1\,x)^{d_1}\,\,d_2^{d_2}} {(d_1\,x+d_2)^{d_1+d_2}}}} {x\,\mathrm{B}\!\left(\frac{d_1}{2},\frac{d_2}{2}\right)}\!$

A closely related distribuiton is the noncentral F distribution.

$p(f) =\sum\limits_{k=0}^\infty\frac{e^{-\lambda/2}(\lambda/2)^k}{ B\left(\frac{\nu_2}{2},\frac{\nu_1}{2}+k\right) k!} \left(\frac{\nu_1}{\nu_2}\right)^{\frac{\nu_1}{2}+k} \left(\frac{\nu_2}{\nu_2+\nu_1f}\right)^{\frac{\nu_1+\nu_2}{2}+k}f^{\nu_1/2-1+k}$

Gamma distribution.

This distribution has two forms.

Gamma distribution

A closely related distribution is the Inverse Gamma distribution.

$\frac{\beta^\alpha}{\Gamma(\alpha)} x^{-\alpha - 1} \exp \left(\frac{-\beta}{x}\right)$

Geometric distribution.

Hypergeometric distribution.

Hypergeometric distribution

Negative binomial distribution.

Negative binomial distribution

Poisson distribution.

Poisson distribution

t distribution.

t distribution

Other resources

Faming Liang, a Professor of Statistics at Texas A&M Univeristy, has some nicely written course notes in PDF format on various distributions as part of his handouts for the STAT 610 course. This includes a derivation of the link between the cumulative probability of a Poisson random variable and percentiles from the Gamma distribution.

This page was written by Steve Simon and is licensed under the Creative Commons Attribution 3.0 United States License. Need more information? I have a page with general help resources. You can also browse for pages similar to this one at Incomplete pages.