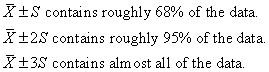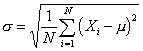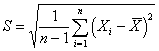StATS: What is a standard deviation? (October 11, 2002)
The standard deviation is a measure of how spread out your
data are. Computation of the standard deviation is a bit tedious. The steps
are:
-
Compute the mean for the data set.
-
Compute the deviation by subtracting the mean from each
value.
-
Square each individual deviation.
-
Add up the squared deviations.
-
Divide by one less than the sample size.
-
Take the square root.
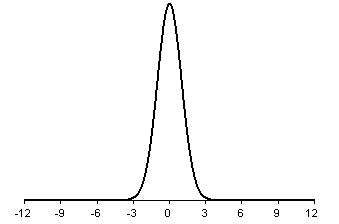
Suppose your data follows the classic bell shaped curve pattern. One
conceptual way to think about the standard deviation is that it is a measures
of how spread out the bell is. Shown below is a bell shaped curve with a
standard deviation of 1. Notice how tightly concentrated the distribution is.
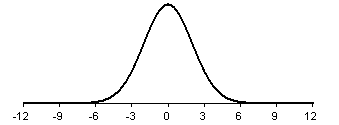
Shown below is a different bell shaped curve, one with a standard deviation
of 2. Notice that the curve is wider, which implies that the data are less
concentrated and more spread out.
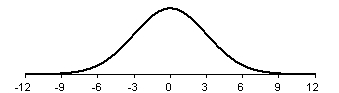
Finally, a bell shaped curve with a standard deviation of 3 appears below.
This curve shows the most spread.
Example
Let's examine a standard deviation computation for data on PI
max values in a sample of children with cystic fibrosis.
The seven values in this data set are 73, 58, 67,
93, 33, 18, and 147. The mean for this data set is 69.9.
| (73-69.9)2 |
= |
(3.1)2 |
= |
9.61 |
| (58-69.9)2 |
= |
(-11.9)2 |
= |
141.61 |
| (67-69.9)2 |
= |
(-2.9)2 |
= |
8.41 |
| (93-69.9)2 |
= |
(23.1)2 |
= |
533.61 |
| (33-69.9)2 |
= |
(-36.9)2 |
= |
1361.61 |
| (18-69.9)2 |
= |
(-51.9)2 |
= |
2693.61 |
| (147-69.9)2 |
= |
(77.1)2 |
= |
5944.41 |
For each data value, compute the
squared deviation by subtracting the mean and then squaring the result.
The sum of these squared deviations is 10,692.87.
Divide by 6 to get 1782.15. Take the square root of this value to get the
standard deviation, 42.2.
Interpreting the standard deviation
For reasonably symmetric and bell shaped data sets:
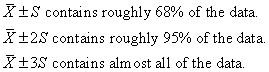
Using SPSS
Select ANALYZE | DESCRIPTIVE
STATISTICS | DESCRIPTIVES from the menu to get computation of the standard
deviation.

This table shows that the
standard deviation is 42.2.
Population standard deviation. The population standard
deviation (often represented by the Greek letter sigma) is measures the
variability of data in a population. It is usually an unknown constant. The
formula is:
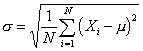
Sample standard deviation. The sample standard deviation
(usually represented by S) measures the variability of data in a sample. It is
easy to compute (compared to a population standard deviation) because it is
based on a small and manageable sample. The formula is:
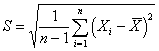
This page was written by
Steve Simon while working at Children's Mercy Hospital. Although I do not hold the copyright for this material, I am reproducing it here as a service, as it is no longer available on the Children's Mercy Hospital website. Need more
information? I have a page with general help
resources. You can also browse for pages similar to this one at Category:
Definitions, Category:
Descriptive statistics.