If you want to quantify the effect of a diagnostic test, you have to first provide information about the patient. You need to specify the pre-test odds: the likelihood that the patient would have a specific disease prior to testing. The pre-test odds are usually related to the prevalence of the disease, though you might adjust it upwards or downwards depending on characteristics of your overall patient pool or of the individual patient.
You are probably more comfortable specifying a probability instead of an odds, and if so there are simple formulas for converting probabilities into odds. You also may have some uncertainty about the pre-test odds. In this case, you might propose a range of values that seem plausible.
You can summarize information about the diagnostic test itself using a measure called the likelihood ratio. The likelihood ratio combines information about the sensitivity and specificity. It tells you how much a positive or negative result changes the likelihood that a patient would have the disease.
The likelihood ratio of a positive test result (LR+) is sensitivity divided by 1- specificity.
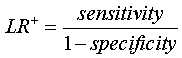
The likelihood ratio of a negative test result (LR-) is 1- sensitivity divided by specificity.
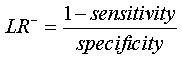
Once you have specified the pre-test odds, you multiply them by the likelihood ratio. This gives you the post-test odds.
![]()
The post-test odds represent the chances that your patient has a disease. It incorporates information about the disease prevalence, the patient pool, and specific patient risk factors (pre-test odds) and information about the diagnostic test itself (the likelihood ratio).
Example
An early test for developmental dysplasia of the hip. The test has 92% sensitivity and 86% specificity in boys (AJPH 1998; 88(2): 285-288). The likelihood ratio for a positive result from this test is 0.92 / (1-0.86) = 6.6 for boys. The likelihood ratio for a negative result from this test is (1-0.92) / 0.86 = 0.09 (or roughly 1/11).
Suppose one of our patients is a boy with no special risk factors. The diagnostic test is positive. What can we say about the chances that this boy will develop hip dysplasia? The prevalence of this condition is 1.5% in boys. This corresponds to an odds of one to 66. Multiply the odds by the likelihood ratio, you get 6.6 to 66 or roughly 1 to 10. The post test odds of having the disease is 1 to 10 which corresponds to a probability of 9%.
Suppose we had a negative result, but it was with a boy who had a family history of hip dysplasia. Suppose the family history would change the pre-test probability to 25%. How likely is hip dysplasia, factoring in both the family history and the negative test result? A probability of 25% corresponds to an odds of 1 to 3. The likelihood ratio for a negative result is 0.09 or 1/11. So the post-test odds would be roughly 1 to 33, which corresponds to a probability of 3%.
Notice that a negative test seems to change things more than a positive test. There are two factors at work here. First, a positive result multiplies the pre-test odds by a factor of only seven whereas a negative result divides the pre-test odds by 11. This means that the test is better at ruling out a condition than ruling it in.
Second, the impact of a test is usually greatest for mid-sized probabilities. If a condition is either very rare, or very common, then only a very definitive test is likely to change things much. But mid-sized probabilities (say between 20% and 80%) will change greatly on the basis of even a moderately precise test.