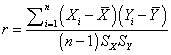
StATS: What is a correlation? (Pearson correlation)
A correlation is a number between -1 and +1 that measures the degree of association between two variables (call them X and Y). A positive value for the correlation implies a positive association (large values of X tend to be associated with large values of Y and small values of X tend to be associated with small values of Y). A negative value for the correlation implies a negative or inverse association (large values of X tend to be associated with small values of Y and vice versa).
The formula for the Pearson correlation
Suppose we have two variables X and Y, with means XBAR and YBAR respectively and standard deviations SX and SY respectively. The correlation is computed as
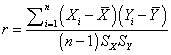
There are some short cuts, but in general the formula is tedious and we will let the computer do all this work.
When will a correlation be positive?
Suppose that an X value was above average, and that the associated Y value was also above average. Then the product
![]()
would be the product of two positive numbers which would be positive. If the X value and the Y value were both below average, then the product above would be of two negative numbers, which would also be positive.
Therefore, a positive correlation is evidence of a general tendency that large values of X are associated with large values of Y and small values of X are associated with small values of Y.
When will a correlation be negative?
Suppose that an X value was above average, and that the associated Y value was instead below average. Then the product
![]()
would be the product of a positive and a negative number which would make the product negative. If the X value was below average and the Y value was above average, then the product above would be also be negative.
Therefore, a negative correlation is evidence of a general tendency that large values of X are associated with small values of Y and small values of X are associated with large values of Y.
Example
Let's compute a correlation coefficient between the 1 minute APGAR scores (X), and the 5 minute APGAR scores (Y). Here's a table showing some of the intermediate calcuations.

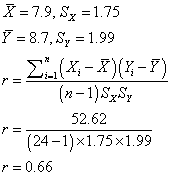
Interpretation of the correlation coefficient.
The correlation coefficient measures the strength of a linear relationship between two variables.
The correlation coefficient is always between -1 and +1. The closer the correlation is to +/-1, the closer to a perfect linear relationship. Here is how I tend to interpret correlations.
This rule, of course, is somewhat arbitrary. For some situations, I mught move the cut-off values closer to 0 (e.g., 0,.2 and 0.6) and for other situations, I might move the cutoff values closer to 1 (e.g., 0.4 and 0.8).
Example of a strong positive association.
The correlation between blood viscosity and packed cell volume is 0.88.
Notice that small volumes tend to have low viscosity and large volumes tend to have high viscosity.
[graph not yet available]
Example of a weak positive association.
The correlation between blood viscosity and fibrogen is 0.46.
Notice that there is also a tendency for small fibrogen values to have low viscosity and for large fibrogen values to have high viscosity. This tendency, however, is less pronounced than in the previous example.
[graph not yet available]
Example of little or no association.
The correlation between blood viscosity and plasma protein is -0.10.
Low levels of protein are associated with both high and low viscosities. High levels of protein are also associated with both high and low viscosities.
[graph not yet available]
Correlation matrix.
When you have more than two variables, you can arrange the correlations between every pair into a matrix.
At the bottom of this page is an example using the blood viscosity data.
To create this table, select ANALYZE | CORRELATE | BIVARIATE from the SPSS menu.
[graph not yet available]
Rounding helps a correlation matrix.
At the bottom of the page is the same correlation matrix, multiplied by 100 and rounded to two significant digits.
We also removed some of the extraneous information.
- - Correlation Coefficients - -
VIS PCV FIB PROT VISCOS 100 88 46 -10 PCV 88 100 42 -16 FIBROGEN 46 42 100 -5 PROTEIN -10 -16 -5 100
Scatterplot matrix.
You can also arrange your scatterplots into a similar pattern.
To create this graph, select GRAPHS SCATTER from the SPSS menu and then select MATRIX from the dialog box.
[graph not yet available]
Interpretation of correlations.
You should be cautious not to overinterpret correlation coefficients. Do not assume that correlation equals causation. Also be careful about how the data was collected. A narrowly restricted sample could lead to a deflation in the correlation.
Correlation does not imply cause and effect.
Sales of rum and number of Methodist ministers is positively correlated, but a large number of ministers does not encourage rum drinking.
Is there a third variable that influences both rum sales and Methodist ministers?
The the previous example, both the sales of rum and the number of Methodists ministers were correlated with the number of people in the U.S. As the number of people increases, it causes an increase in demand for both Methodist ministers and for rum.
If you adjusted for the number of people, for example by computing the sales of rum and the number of ministers per capita, then the association would disappear.
There are many examples where a high correlation between two variables can be explained by a third factor. Always look for an alternate explanation of the correlation.
For example, hay yields are negatively correlated with the average springtime temperature. This seems counterintuitive. But it is easy to understand once you realize that hay yields are highly dependent on springtime rainfalls. And a rainy Spring is usually cooler than a dry Spring.
Restriction of range.
If one of your variables has an artificially restricted range, then the correlation will be pushed closer to zero.
The correlation between 1m inute and 5 minute APGAR scores is 0.66.
If we restrict the data set to babies with one minute APGAR > 5, then the correlation declines to 0.25.
There is a lot of debate about how important SAT scores are at predicting an individual's success in college. Most colleges have information about the SAT scores of their students and measures of their success, such as their grade point average during their sophomore year.
This data, however, provides uncertain evidence of the relation between SAT scores and grades. Most colleges restrict their enrollees to have higher than a certain range for the SAT. For some colleges, this can lead to a very narrow range of SAT scores. When these data show a poor correlation, it is unclear whether this is caused by the artificial restriction in the range of SAT scores.
A better, but perhaps impractical, way to assess this situation is for the college to admit all entrants regardless of SAT and then see whether there is a correlation between SAT scores and GPA.
This page was written by Steve Simon while working at Children's Mercy Hospital. Although I do not hold the copyright for this material, I am reproducing it here as a service, as it is no longer available on the Children's Mercy Hospital website. Need more information? I have a page with general help resources. You can also browse for pages similar to this one at Category: Definitions, Category: Measuring agreement.