
Continuous variables in a logistic regression model (February 9, 2005).
This page is moving to a new website.
I got a question by email that asked, in a rather indirect way, how to interpret the odds ratio estimate for a continuous variable in a logistic regression model. It turns out that the odds ratio represents a change in the estimated odds of the outcome when the continuous variable increases by one unit. See
for a more detailed discussion of this interpretation.
I failed to mention in that web page how important the measurement scale is in this situation. If you use grams as a unit of weight rather than kilograms, then you will be estimating a relative change in odds per gram change in weight, which is often so small that it is difficult to make sense out of it.
Here's an example computed from the bf.sav file that I use in several of my training classes:

The dependent variable is exclusive breast feeding at discharge, and birth weight in grams has a highly significant effect on the outcome (p=0.005). But notice that the estimated odds ratio is very close to 1. It turns out that the estimated odds of exclusive breast feeding at discharge increase by 0.2% for every increase in birth weight by one gram. This is rather hard to interpret.
If you refit the model using birth weight in kilograms, you get the same p-value, but now the odds ratio is much easier to interpret.
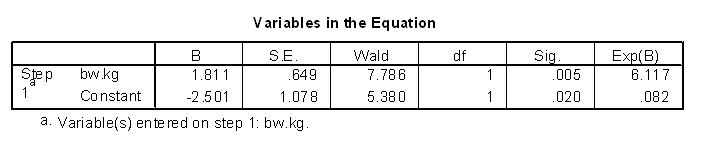
The odds of exclusive breast feeding at discharge increase six fold when the birth weight increases by one kilogram.
You need to be a bit cautious about these findings because the research study was restricted to pre-term births, but clearly the interpretation is much easier using kilograms rather than grams.
In theory, you could convert from one odds ratio to the other by raising 1.002 to the 1,000 power, but this calculation is difficult to perform and is subject to rounding error. A better way to make the conversion would be to take the log odds ratio (0.002) and mulitply that by 1,000 and then exponentiate the result. Even then, you would have considerable rounding error because of the way SPSS displays the log odds ratio.