This page has moved to my new website.
One of my favorite people to work with, Vidya Sharma, was asking me how to compute the sample size in a cluster randomized trial. I had started to write a web page about this, but never found the time to finish it.
A cluster randomized trial selects several large groups of patients and then randomly assigns a treatment to all of the patients within a group. A cluster randomized trial requires a larger sample size than for a simple randomized trial. You always want as much homogeneity between the treatment and control group. Homogeneity insures an apples to apples comparison. Clusters also have homogeneity, and your inability to randomize within a cluster means a missed opportunity to improve the homogeneity of the treatment versus control comparison.

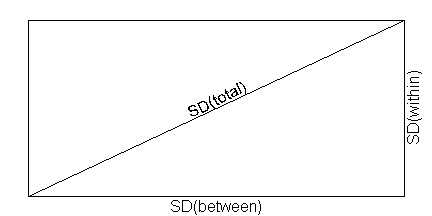
This figure illustrates how between and within standard deviations contribute to the overall variation. The standard deviations combine in a Pythagorean way:
![]()
The intraclass correlation (ICC) is a measure of homogeneity within clusters. The formula is
![]()
If the ICC is large and/or if you have very large cluster sizes, then cluster sampling will be inefficient. The design effect (DEFF) which is also called the inflation factor is a measure of the inefficiency. The formula for DEFF is
![]()
To estimate the total sample size in a cluster sample, first estimate an unadjusted sample size using the traditional formula. For example, the sample size for comparing two binomial proportions is
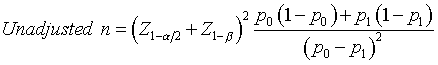
Then multiply this sample size by the DEFF to get your adjusted sample size.
![]()
The number of clusters, c, is just
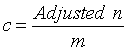
A publication in the International Journal of Epidemiology takes a different perspective. It computes a factor k, which represents the between cluster coefficient of variation. If you are comparing two means, the traditional sample size formula is
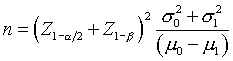
but under a cluster sample with clusters of size m, you would need to sample c clusters per group where
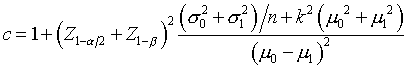
You can think of the k factor as a penalty for the cluster sample and if k=0, there is effectively no penalty. As k, the between cluster coefficient of variation, increases, you will need more and more data to compensate for the increasing amount of homogeneity within clusters.
The formulas for sample sizes with proportions and with rates work similarly.
Cluster randomised trials in maternal and child health: implications for power and sample size. Reading R, Harvey I, Mclean M. Arch Dis Child 2000: 82(1); 79-83.
Statistical and design issues in studies of groups. Accounting for within-group correlation. Cummings P, Koepsell TD. Inj Prev 2002: 8(1); 6-7. [Full text] [PDF]
Simple sample size calculation for cluster-randomized trials. R. J. Hayes, S. Bennett. Int J Epidemiol 1999: 28(2); 319-26. [Medline] [Abstract] [PDF]
Sample size formulae for intervention studies with the cluster as unit of randomization. Hsieh FY. Stat Med 1988: 7(11); 1195-201. [Medline]
Sample Size and Design Effect: Introduction and Review [PDF]. Shackman G, Newsletter of the Survey Research Methods Section, January 2003, page 8. Accessed on 2003-05-08. www.amstat.org/sections/srms/January2003Newsletter.pdf
Sample size and design effect [PDF]. Shackman G, Albany Chapter of the American Statistical Association 2001 conference. Accessed on 2003-05-08. www.albany.edu/~areilly/albany_asa/confweb01/abstract/Download/shackman.pdf
Additional links: