One of the people I work with is always looking for hidden subgroups in his data. For him, this is a starting point for exploring for genetic variations.
That's an admirable activity, but it is remarkably difficult to thing to do in practice. The first step is to see if the distribution of values for some measurement has a bimodal distribution. A second mode is an indication of a subgroup of patients that may have a genetic variation from the rest of the patients.
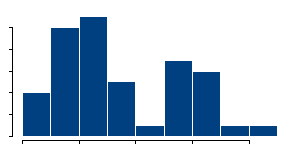
A histogram, like the one shown above is a quick and simple way to look for bimodality. The problem is that histograms are very sensitive to how thick
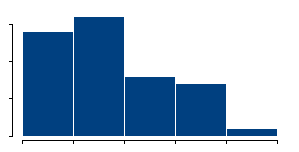
or thin
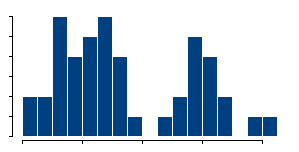
the bars are. Indications for bimodality may appear or disappear depending on how you draw the histogram.
A QQplot is much better because it is not dependent on bar widths.
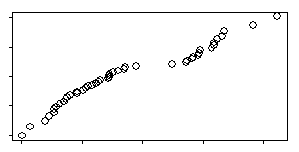
The QQplot compares your data to evenly spaced percentiles from a normal distribution. If you had nine data values, the smallest one would be compared to the 10th percentile, the next smallest one to the 20th percentile and so forth, until the largest one was compared to the 90th percentile of a normal distribution.
A straight line on the QQplot indicates data that is well approximated by a normal distribution. If instead you see two distinct lines, then this is a possible indication of bimodality.
Interpretation of the QQplot is somewhat subjective, and we all have a tendency to overinterpret small deviations. One way to quantify this calculation is to compute a correlation between the data and normal percentiles. This will always be large, but if it is very close to +1, that indicates normality. A slightly smaller value indicates non-normality of one form or another. It might actually be something like skewness instead of bimodality, so further investigation would be needed.
The correlation does not have to be that much smaller than 1 to indicate non-normality. A value of 0.90 or even 0.95 might be sufficient evidence. There are tables for this, but you can quickly compute a critical value yourself.
In the example shown above, there are 46 observations. The correlation between the data and the normal scores is 0.969.
So let's compute 46 observations that really do come from a single normal distribution and see how they behave. Here's some S-plus/R code to do this calculation
x <- rnorm(46)
z <- qnorm(rank(x)/47)
cor(x,z)
[1] 0.9803026
Notice that the batch of perfectly normal data did indeed have a correlation closer to one. Let's repeat this a thousand times and see what happens.
co <- rep(NA,1000)
for (i in 1:1000) {
x <- rnorm(46)
z <- qnorm(rank(x)/47)
co[i] <- cor(x,z)
}
mean(co)
[1] 0.9879957
So the average correlation when the data is perfectly normal is much higher than the value we observed.
quantile(co,probs=0.05)
5%
0.9738147
Even the fifth percentile of these correlations is still larger than 0.969. So we would conclude that there is some evidence of non-normality and would then investigate further to see if it was indeed bimodality.
The formal statistical tests for bimodality are quite complex, but I will try to illustrate them when I get a chance.